
Les piscine sont fermées à cette période de l'année, mais la mer et la plage, à 100 mètres à pied de la résidence, peuvent tenter l'un ou l'autre pendant la pause méridienne. D'après les prévisions météo, les deux premières journées verront un peu de ciel dégagé, mais le véritable soleil ne reviendra qu'après la fin des cours, malheureusement.
Comment venir à la résidence ?
La résidence Odalys - La Londe les Maures se trouve dans le département du Var. L'adresse postale est : 395 Boulevard de la plage de l’Argentière, 83250 La Londe les Maures.
En train
Nous avons prévu des bus navettes entre les gares Aix-en-Provence TGV et Toulon et la résidence, la gare SNCF la plus proche à Hyères étant assez mal désservie.
Horaires navettes Arrivée
Aix-en-Provence TGV : 13h30
Toulon, gare SNCF et gare routière : 14h30
Horaires navettes Départ
L'organisation du départ est soumis à modification en fonction des besoin des participants.
Départ de la résidence Odalys au plus tard 13h45, soit une navette Toulon-Aix, soit une navette pour chaque destination.
Arrivée Aix-en-Provence TGV : 16h00
Arrivée aux gares de Toulon : 14h30
En avion
L'aéroport Toulon-Hyères (IATA code TLN) se trouve à 20' en voiture de la résidence Odalys.
Navettes (extrait de varlib.fr) - ligne 7803
- Arrivée : aéroport TLN 13h35 - 13h55 centreville de La Londe (2km de la résidence)
- Départ : centreville 15h10 - 15h25 aéroport TLN
Les aéroports « Marseille-Provence » (IATA codes MRS et MP2) se trouvent à 10' en voiture de la gare Aix-en-Provence TGV et à une demi-heure de la gare principale Marseille-St. Charles.
Navettes (détails sur marseille.aeroport.fr)
- Aix en Provence TGV : toutes les 30' (deux stations)
- Marseille St. Charles : toutes les 20' (heures creuses) à 15'
En voiture
Coordonnées GPS : 43,125°N 6,254°E
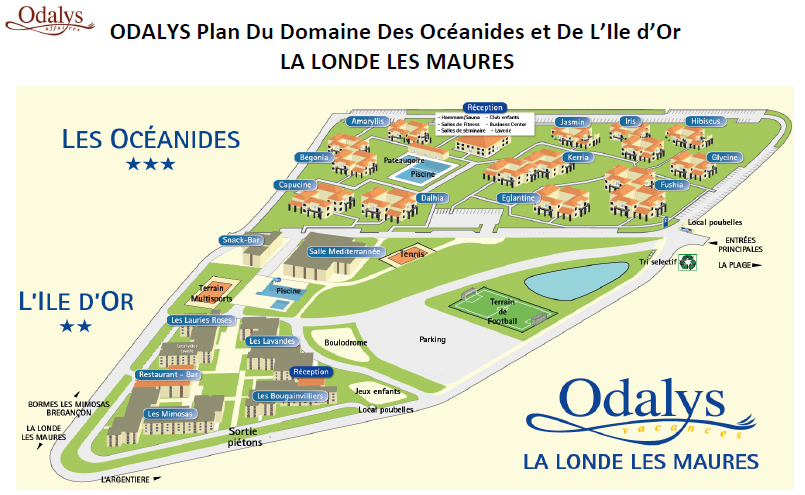
Et à l'arrivée ?
Lors de votre arrivée mardi, vous êtes priés de vous rendre directement en salle des cours (le bâtiment "Réception" en haut du plan). Vous y trouverez également l'accueil qui ouvrira ses comptoirs à partir de 18h. La « pause » entre 18h et 19h est prévue pour occuper vos chambres, résoudre éventuellement de derniers problèmes avec les VM et prendre un apéritif. La suite est décrite dans le programme.

